An Idiot’s Guide to ACES

I’ve been putting off working in ACES for years now, because almost every explanation of the system I’ve tried to read online has been either extraordinarily technical and long-winded, or read like a sales pitch with no useful information about implementation. It takes a certain amount of training and understanding to get a team of artists to work with ACES reliably, and so to save my own sanity I just stuck with the usual “linear workflow” and tried not to worry about it. Now that I’m running a much smaller team at my current job, I decided it was time to actually try to implement ACES for real, and this is my attempt at writing down what I’ve learned into a practical guide for why and how you should implement ACES in your own work. I’m probably (definitely) over-simplifying plenty of details, but that’s what all the long and boring technical guides that smarter people have written are for. Feel free to yell at me in the comments if you like.

An important note: I’m a (technical) 3D production artist, not a color scientist. The “Idiot” in this Idiot’s Guide is me. I’m just trying to translate a lot of difficult jargon and theory into something that’s practical for use by normal humans, because I could barely make any sense out of it myself. I’m likely taking shortcuts and making compromises in certain places that would make a Real Color Scientist’s eyes bleed, but that’s the nature of production… sometimes you have to break the rules to get the image the client wants.

WTF is ACES?

ACES is a color system that’s meant to standardize how color is managed from all kinds of input sources (film, CG, etc), and provide a future-proof working space for artists to work in at every stage of the production pipeline. Whatever your images are coming from, you smoosh them into the ACES color standard, and now your whole team is on the same page.

For CG artists, a big benefit is the ACEScg color gamut, which is a nice big gamut that allows for a lot more colors than ye olde sRGB. Even if you’re working in a linear colorspace with floating-point renders, the so-called “linear workflow”, your color primaries (what defines “red”, “green” and “blue”) are likely still sRGB, and that limits the number of colors you can accurately represent.

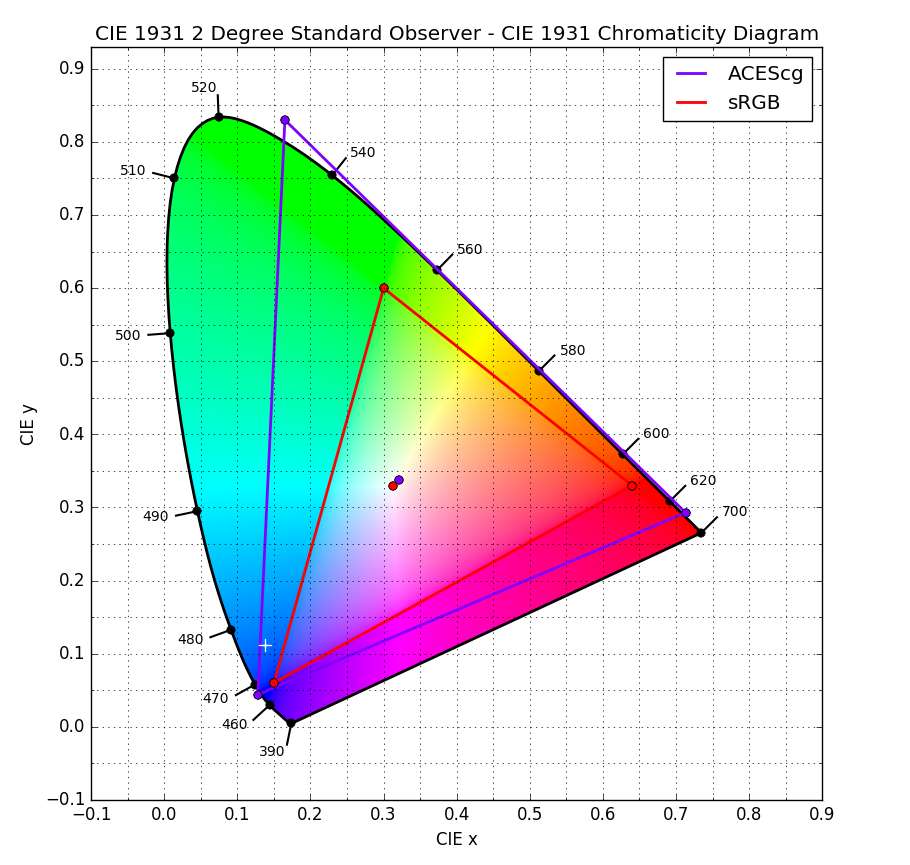
What we typically think of as “linear” versus “sRGB” is a bit of a misnomer… a linear colorspace can use sRGB primaries, which is what most of us outside of ACES are dealing with when we’re working with “linear” textures or renders. What we usually call “sRGB” is also using the sRGB primaries, but with a 2.2 gamma curve applied in order to make it display properly on typical monitors. ACEScg, on the other hand, uses its own set of primaries called “AP1”, which allows for that nice big triangle o’ colors in the diagram above. Remember that the sRGB / Rec. 709 standard was developed back when we were still using CRT monitors and wearing acid washed jeans. It’s time to put away your NKOTB World Tour t-shirt.

Here’s a quick example showing you the difference between a render in your typical sRGB “linear” workflow, and an ACES workflow. You can tell right away that the colors you get are significantly more “real”, especially at the extremes of brightness and saturation.

• 

• 

ACEScg is the ACES color space of choice to use for CG artists because it’s linearly encoded (as opposed to logarithmically, which tends to be how non-CG people like to think about exposure), so your render engine and compositing program of choice will play nicely with it. There are other color spaces defined in the ACES specification, including the ACES 2065-1 space for archival and interchange purposes, but as a CG artist the only one you really need to worry about for now is ACESCG.

The Viewer LUT

So, we know we have ACESCG as the color space we want to work in. However, your crappy monitor can’t display this whole space. Even if you have a nice monitor, it can probably only accurately display the DCI-P3 gamut, which is still not as big as ACESCG. The other space you need to define, then, is your “viewing” space. This is kind of like when you’re looking at a linear render and everything appears way too dark until you hit the “sRGB” or “gamma 2.2” button… the image needs to be transformed from whatever color space it’s rendered in to a space that your monitor likes. This viewing space is dependent on your own monitor situation, but if you’re not on a fancy monitor, it’s probably either sRGB or Rec. 709 (the two are very very similar). You’ll need to make sure that when you’re viewing or compositing your renders that you’re looking through the right viewer LUT that transforms your renders from ACESCG to sRGB or Rec. 709 or Rec. 1886 or whatever you’re into.

One other thing… the “Output” color spaces in ACES have something called an “RRT” involved, which stands for “Reference Rendering Transform”. This is an overly-technical way of saying that there is an extra transformation happening between your ACEScg scene and your sRGB or Rec 709 viewer space! The RRT is similar to your typical S-curve that you’d apply to renders or footage to get nice deep blacks and rolled-off highlights. It looks great, but it can introduce complexities later on when you’re trying to get exact output colors from a matching input… which frequently is a necessity in commercials when you’re matching brand colors or compositing screens onto objects. More on this in a bit.

Converting Input Textures

You’ll also need to make sure that any applicable color textures you’re using are converted into the ACEScg color space. This part can be tricky, because textures can come from a wide variety of sources. You’ll need to apply what’s called an “input device transform”, or “IDT”, to these textures. Most textures you download from the internet are going to be in the sRGB color space, which you’ll see in OCIO as “Utility – sRGB – Texture”. If you have nice linear EXR textures or renders, your IDT would instead be Utility – Linear – sRGB. The naming here is of course confusing, because everything about color is confusing, but the Linear – sRGB there means that you’re dealing with an image that is rendered with linear values, i.e. no tonemapping curve, but using sRGB primaries. Your typical JPEG is also using sRGB primaries, but it has an input gamma curve of 2.2, so it’s not linear.

When in doubt, if the image isn’t floating-point, use Utility – sRGB – Texture. If it is floating-point, use Utility – Linear – sRGB.

Color swatches are no different! You’ll need to make sure that the values you’re inputting, if you’re not converting them directly through an OCIO transform node in your software of choice, are in the ACEScg space.

Now, above I used the qualifiers “applicable” and “color” when describing textures that you need to convert to the ACEScg color space. What I mean by this is that you only want to convert textures that describe color, and not textures that describe data. A diffuse or albedo texture map describes color and needs to be color-corrected. A normal, displacement, or roughness map describes data and should NOT be converted. It’s important to keep this distinction in mind when color-correcting your input textures!

How to actually set up ACES

First off, you need to download the actual definition of these fancy ACES color spaces. The easiest way to do this is to use the OpenColorIO (OCIO) configuration. You can download it here: https://github.com/colour-science/OpenColorIO-Configs

Inside you’ll find several different ACES configurations. I’m using v1.0.3 here. In the aces_1.0.3 folder, you’ll find a file called “config.ocio”… this is the main file you’ll be pointing to in other applications that can use ACES. Some applications like Fusion have in-app controls to allow you to specify an OCIO configuration file, but in general the easy way is to set up the OCIO system environment variable. You just need to set OCIO=/path/to/config.ocio, depending on where you’re storing the config.ocio file. On Windows, you can do this through Control Panel > System Properties > Advanced > Environment Variables. On Linux or OSX, you want to use the “export” shell command like so:

export OCIO=/path/to/config.ocio

If you want this to apply permanently, you can add the line to your user’s “.bash_profile” file, found at ~/.bash_profile, using any text editor. Start a new shell or logout/login again to apply the change.

Most relevant 3D and compositing applications will recognize this OCIO variable automatically, and so you can move onto configuring the exact color spaces you want to use per-application.

Configuring your applications

Next, you need to configure your application. This is where things can start to get complicated, because the exact setup procedure is different depending on what app you’re using, and what render engine you’re using. I’ll include a few examples of common applications here.

Maya

Maya has built-in color management now, though not every supported render engine is compatible with it (I’m looking at you, Redshift!) To use it, go to Maya’s preferences, Settings > Color Management, and check Enable Color Management and Use OCIO Configuration. If the OCIO Config Path isn’t filled in, set it to the path of the config.ocio file you downloaded earlier. Once that’s set up, you can define your “Rendering Space” and your “View Transform”. The Rendering Space should be our new friend ACEScg. The View Transform is your “viewer” space… for most of you this is sRGB or Rec. 709, depending on your monitor. Finally, you can set up a list of default rules for how you want Maya to handle input textures, based on the file extension or the path on disk. Remember that these rules are just guesses, and will not be smart enough to tell the difference between a color texture (convert this!) and a data texture (do not convert this!) unless you set up your file path structure on disk to enforce these rules! You’ll likely have to manually adjust the color transform settings on your File nodes on certain textures. The important part is to just be aware of the input color space of your textures, and don’t rely on the automated rules to do this thinking for you.

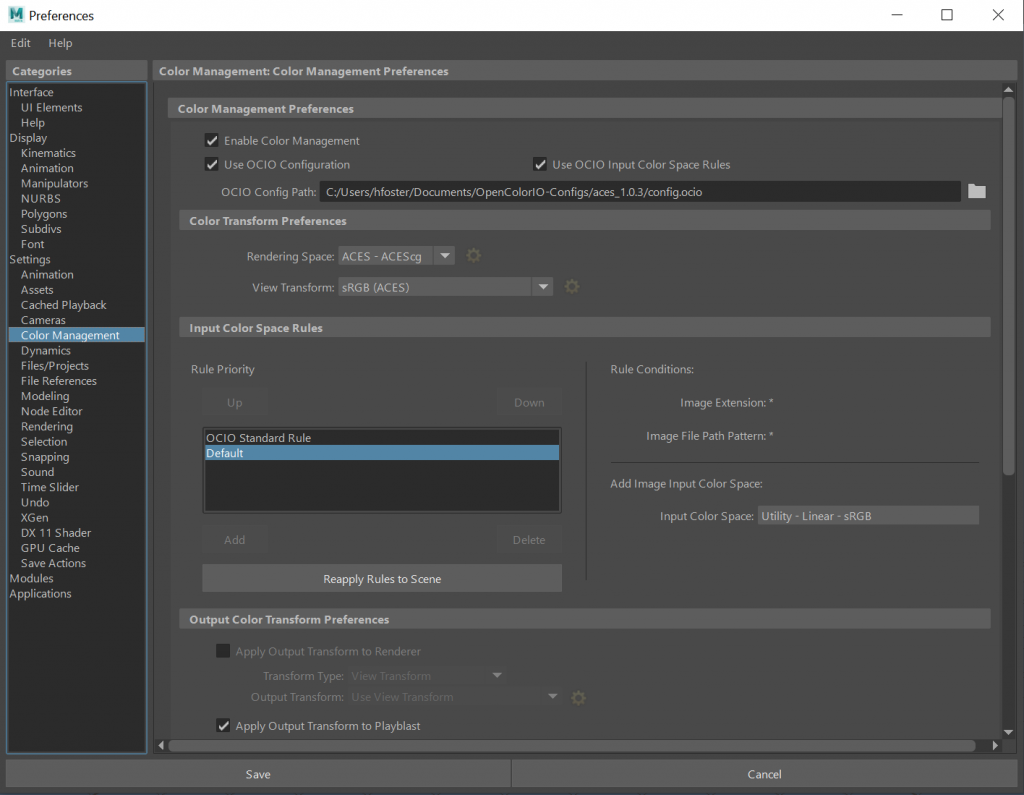
Finally, you need to configure your Render View to display your renders through the correct LUT. This is different per-render engine. In Redshift, this is configured in the “Redshift Post Effects” settings, available via Render Settings > Color Management, or from the Redshift Render View by clicking the gear icon at the upper right of the Render View window (expand the window if you can’t see it), then looking for the Color Management dropdown.

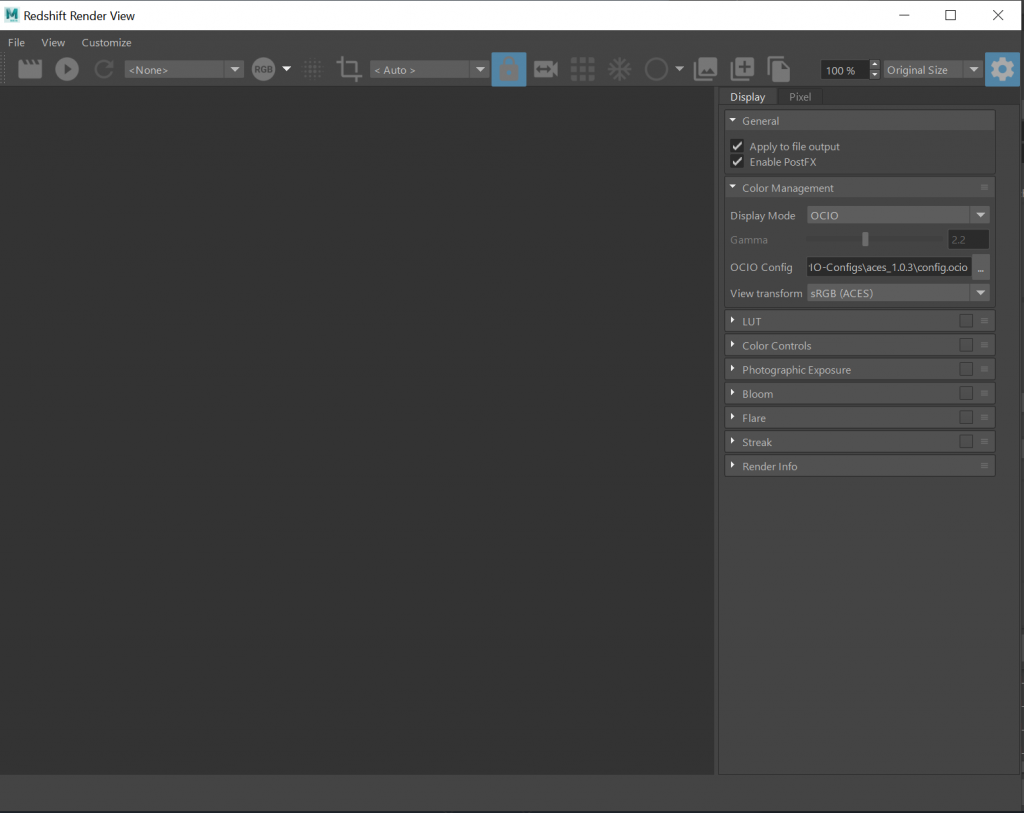
Of course, Redshift (and probably some other render engines I don’t use) don’t yet support Maya’s internal color management system. In cases like this, you’ll want to disable Maya’s color management, and you’ll have to convert your textures manually outside of Maya. The two easiest ways to handle this are the “ocioconvert” tool that comes packaged with OpenImageIO (https://github.com/OpenImageIO/oiio), or a compositing application like Blackmagic Fusion or Nuke. The rules are otherwise the same… transform the input texture from the appropriate input space (Utility – blah blah blah) to the ACEScg space, then save the file.

Houdini

If you’ve set the OCIO environment variable, Houdini’s Render View should automatically show a list of available ACES display LUTs at the bottom, along with the exposure and channel masking controls (these are hidden by default; just click the little ridge at the bottom of the render view window if you don’t see them). You can use the OCIO Color Transform VOP to transform input textures from the appropriate input spaces to ACEScg.

Again, some render engines may not natively support the OCIO Color Transform VOP, and in these cases you’ll have to color correct your textures manually. Since you have Houdini, you can use COPs to transform your textures natively rather than relying on OpenImageIO or an external compositing program to convert them. Redshift currently doesn’t support it, and Mantra’s built-in ubershaders (the Principled and Classic shaders) have their own built-in color correction assumptions that don’t seem to lend themselves to in-line color transforms in the MAT context. It’s probably safest (and fastest) to pre-convert your textures into ACEScg before rendering.

Something to keep in mind specifically when using the File COP in Houdini is that it tries to linearize your textures for you! You can either change your OCIO Transform VOP’s input space to Utility – Linear – sRGB, or uncheck “Linearize Non-Linear Images” on the File COP. You’ll also want to change the “File Raster Depth” to be “Specific Depth” and set the Depth to either 16- or 32-bit floating point. You don’t want to be writing 8-bit images in ACEScg.

Fusion

If the OCIO environment variable is set, Fusion should automatically list the “OCIO ColorSpace ViewLUT” in the list of available LUTs at the bottom of each viewer. Click the “LUT” button to enable a viewer LUT, then click the arrow next to it and select the OCIO ColorSpace ViewLUT, then go to Edit… to set your source and output spaces. Your source space is always going to be ACES – ACEScg. Your output space, as always, depends on your monitor… this will likely be “Output – Rec. 709” or “Output – sRGB”.

With these settings, you can just import ACEScg renders and composite like you normally would, since ACEScg is a linear space. However, if you have other footage going into the comp that is not ACEScg, you’ll need to use the OCIOColorspace node to transform the footage from the appropriate space to ACEScg. You can use the same rule of thumb for most footage… if it’s an LDR image, it’s probably “Utility – sRGB – Texture”, and if it’s HDR it’s probably “Utility – Linear – sRGB”.

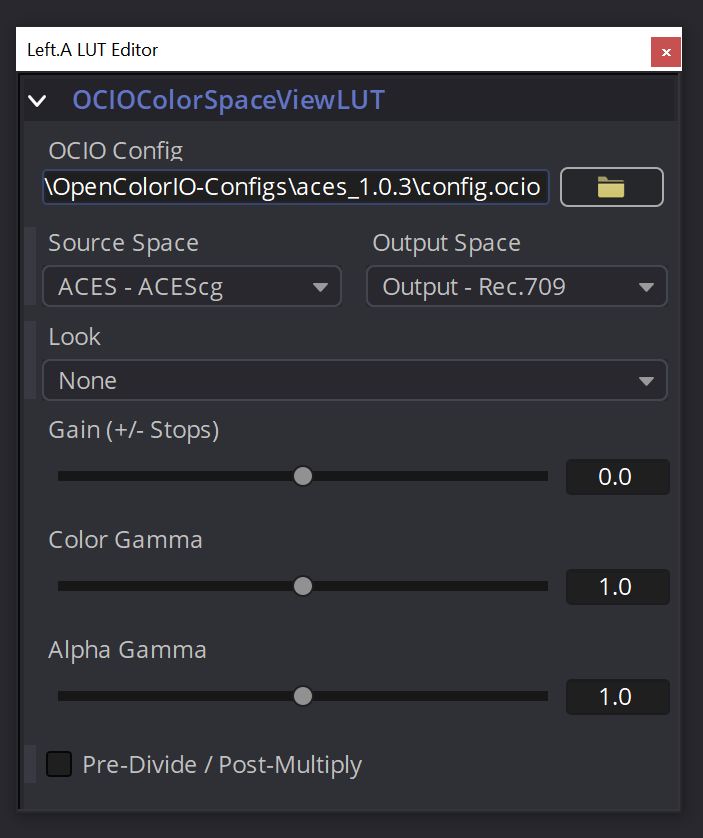
Finally, when writing your comp to disk, you’ll likely need to do another color transform. The space to write to is dependent on your own local color pipeline. If you’re delivering to the web, mobile, or typical TVs, you’ll probably be converting to Rec. 709. If you’re delivering an HDR spot, you might be converting to Rec. 2020. If you’re trying to write out final images to DI and they want to be super-ACES-compliant, you’ll render to the archival ACES2065-1 space. If in doubt, ask your colorist. Use the OCIOColorspace node to transform to the output color space before your Saver node. If the image looks weird when you preview this node, it’s because your viewer LUT is still enabled… you can disable it to check your colors before writing if you’re paranoid.

Nuke

You can set your working color space in Nuke under Project Settings > Color. Your working space is ACEScg. Your “monitor” space is the same as your “viewer” space mentioned above… this will likely be “sRGB” or “Rec. 709” if you have a typical monitor. You can set presets for incoming footage below… 8-bit files should default to “Utility – sRGB – Texture”, and float files to ACEScg. Just remember that if you’re importing float files that didn’t come from one of your ACEScg renders, you’ll need to use an OCIOFileTransform node to convert from the appropriate space (probably “Utility – Linear – sRGB”) to ACEScg.

Before writing final images to disk, use the OCIOFileTransform node to convert your comp into the appropriate delivery color space. See the “Fusion” section above for hints on what color space you might want to write to.

Annoying ACES gotchas

Of course, aside from having to read articles like this one, there are certain annoyances with the ACES system, especially for those of us that are frequently rendering things that aren’t necessarily “realistic”. The biggest problem I’ve run into is trying to get the result of an ACES render or comp to match a reference image… for example, a matte painting or a phone screen that needs to be tracked onto a device, or anything self-illuminated that isn’t actually acting like a light. If you just apply the usual sRGB -> ACEScg conversion, you’ll notice that your self-illuminated material appears muted in renders.

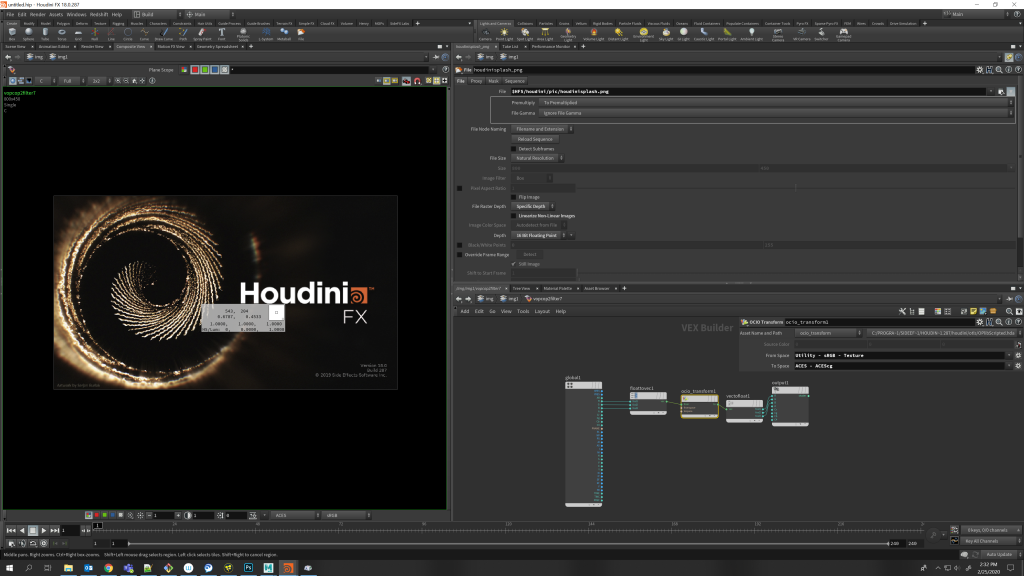
In situations like this, you have a couple of options, depending on where in the process you are. If you need a self-illuminated material in 3D to appear in renders exactly as it appears when you view the texture outside of ACES, you need to convert the texture to ACEScg, but from the OUTPUT space rather than the usual input space. This means that if your viewer is using the “Output – sRGB” space, you want to use this as your texture’s input space. This will ensure that, perceptually, the opposite of your viewer LUT, including the RRT S-curve tonemapping mentioned earlier, will be applied to your texture, so it will look exactly the same coming out the other side of ACES. This means that your output color values might come out pretty weird! Take a look at this screenshot and pay close attention to both the OCIO Transform settings and the color info window that appears over the render on the left.

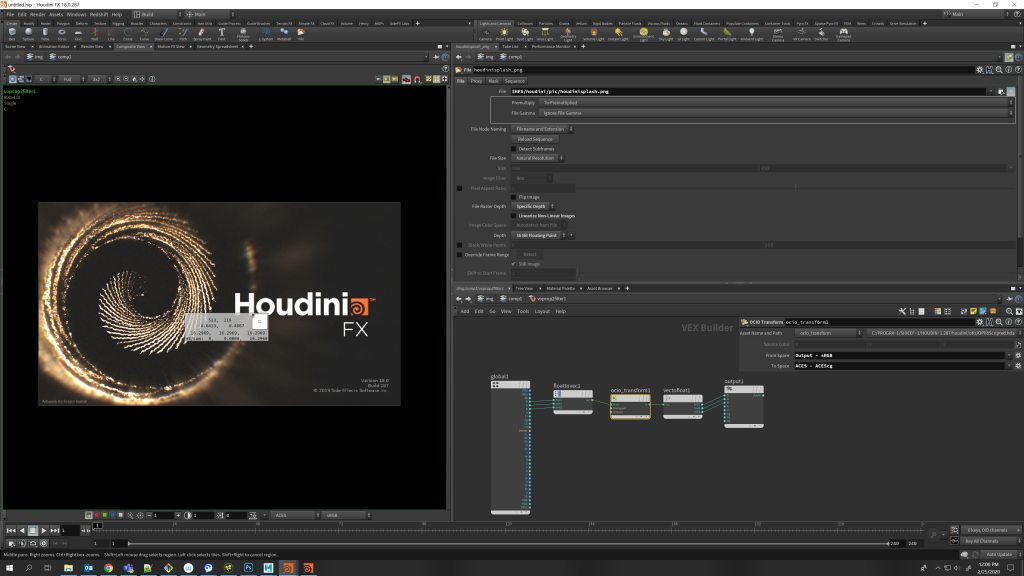
In the above screenshot, what you’re seeing as “white” is actually a value of about 16. Other colors might also be affected in strange ways by this process, especially when dealing with very bright or saturated colors. Keep numbers like this in mind when debugging issues with global illumination or weird reflections or other render glitches, or when grading these renders after rendering!

On the compositing side, your best option for solving this same problem is simply exiting ACEScg space temporarily. This is best done near the end of your comp, for obvious reasons. Use the OCIO transform tools to convert from ACEScg to sRGB, change your viewer LUT to view in standard sRGB, then comp in your sRGB elements like screens, subtitles, end cards, etc. This has the advantage of avoiding the aforementioned wacky color values, but can cause problems down the line if you’re trying to output to an HDR delivery target, and you’ll need to make sure that your colors don’t screw up if you have to output to Rec. 2020 or ACES2065-1 or ACEScc or whatever.

Closing Thoughts

Even for what’s supposed to be a quick and practical guide, this is obviously a bit of reading. The ACES system is a good idea, but its implementation is still difficult and counter-intuitive, and it requires that everyone on your art team has an understanding of what color spaces to convert to and when to convert (or when not to). I hope this write-up at least gets you to understanding the basics of the system, and when you’re ready for the deep dive, I highly recommend you read the following guides:

ACES Primer: https://acescentral.com/uploads/default/original/1X/6ad8b74b085ac8945c1e638cbbd8fdf687b7f60e.pdf

Chris Brejon’s ACES Guide: https://chrisbrejon.com/cg-cinematography/chapter-1-5-academy-color-encoding-system-aces/

Special thanks goes to Hernan Santander, Joe Pistono, Lewis Saunders, and Robert LaPlante for helping me make sense of all this ridiculous color business.